面试官:说说你对函数式编程的理解?优缺点?
一、是什么
函数式编程是一种"编程范式"(programming paradigm),一种编写程序的方法论
主要的编程范式有三种:命令式编程,声明式编程和函数式编程
相比命令式编程,函数式编程更加强调程序执行的结果而非执行的过程,倡导利用若干简单的执行单元让计算结果不断渐进,逐层推导复杂的运算,而非设计一个复杂的执行过程
举个例子,将数组每个元素进行平方操作,命令式编程与函数式编程如下
// 命令式编程
var array = [0, 1, 2, 3]
for(let i = 0; i < array.length; i++) {
array[i] = Math.pow(array[i], 2)
}
// 函数式方式
[0, 1, 2, 3].map(num => Math.pow(num, 2))// 命令式编程
var array = [0, 1, 2, 3]
for(let i = 0; i < array.length; i++) {
array[i] = Math.pow(array[i], 2)
}
// 函数式方式
[0, 1, 2, 3].map(num => Math.pow(num, 2))简单来讲,就是要把过程逻辑写成函数,定义好输入参数,只关心它的输出结果
即是一种描述集合和集合之间的转换关系,输入通过函数都会返回有且只有一个输出值
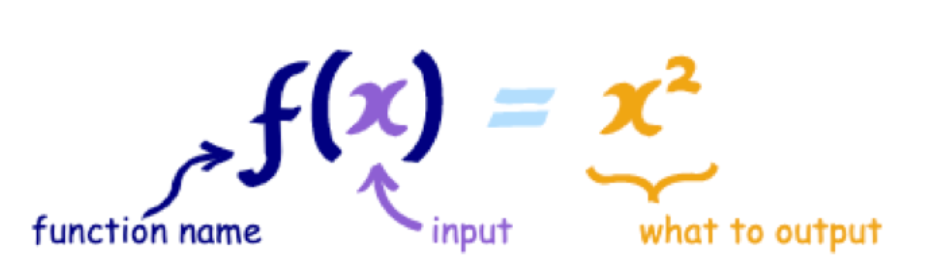
可以看到,函数实际上是一个关系,或者说是一种映射,而这种映射关系是可以组合的,一旦我们知道一个函数的输出类型可以匹配另一个函数的输入,那他们就可以进行组合
二、概念
纯函数
函数式编程旨在尽可能的提高代码的无状态性和不变性。要做到这一点,就要学会使用无副作用的函数,也就是纯函数
纯函数是对给定的输入返还相同输出的函数,并且要求你所有的数据都是不可变的,即纯函数=无状态+数据不可变
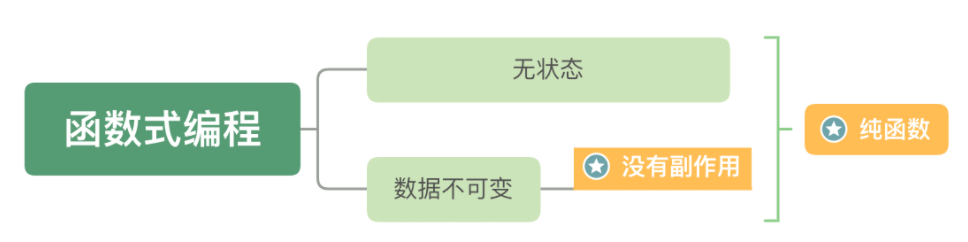
举一个简单的例子
let double = value=>value*2;let double = value=>value*2;特性:
- 函数内部传入指定的值,就会返回确定唯一的值
- 不会造成超出作用域的变化,例如修改全局变量或引用传递的参数
优势:
- 使用纯函数,我们可以产生可测试的代码
test('double(2) 等于 4', () => {
expect(double(2)).toBe(4);
})test('double(2) 等于 4', () => {
expect(double(2)).toBe(4);
})不依赖外部环境计算,不会产生副作用,提高函数的复用性
可读性更强 ,函数不管是否是纯函数 都会有一个语义化的名称,更便于阅读
可以组装成复杂任务的可能性。符合模块化概念及单一职责原则
高阶函数
在我们的编程世界中,我们需要处理的其实也只有“数据”和“关系”,而关系就是函数
编程工作也就是在找一种映射关系,一旦关系找到了,问题就解决了,剩下的事情,就是让数据流过这种关系,然后转换成另一个数据,如下图所示
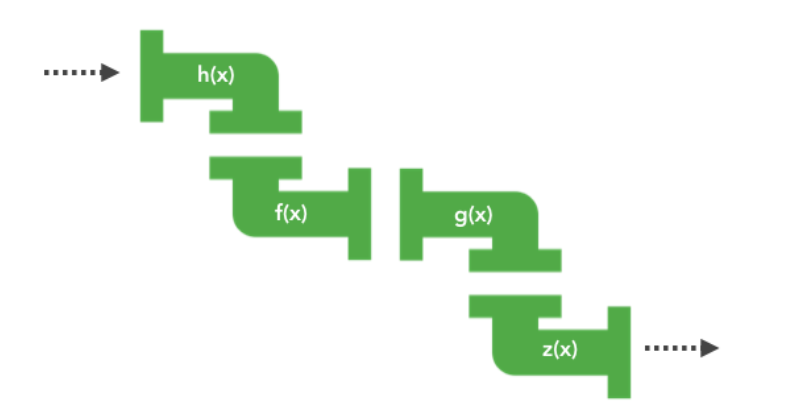
在这里,就是高阶函数的作用。高级函数,就是以函数作为输入或者输出的函数被称为高阶函数
通过高阶函数抽象过程,注重结果,如下面例子
const forEach = function(arr,fn){
for(let i=0;i<arr.length;i++){
fn(arr[i]);
}
}
let arr = [1,2,3];
forEach(arr,(item)=>{
console.log(item);
})const forEach = function(arr,fn){
for(let i=0;i<arr.length;i++){
fn(arr[i]);
}
}
let arr = [1,2,3];
forEach(arr,(item)=>{
console.log(item);
})上面通过高阶函数 forEach来抽象循环如何做的逻辑,直接关注做了什么
高阶函数存在缓存的特性,主要是利用闭包作用
const once = (fn)=>{
let done = false;
return function(){
if(!done){
fn.apply(this,fn);
}else{
console.log("该函数已经执行");
}
done = true;
}
}const once = (fn)=>{
let done = false;
return function(){
if(!done){
fn.apply(this,fn);
}else{
console.log("该函数已经执行");
}
done = true;
}
}柯里化
柯里化是把一个多参数函数转化成一个嵌套的一元函数的过程
一个二元函数如下:
let fn = (x,y)=>x+y;let fn = (x,y)=>x+y;转化成柯里化函数如下:
const curry = function(fn){
return function(x){
return function(y){
return fn(x,y);
}
}
}
let myfn = curry(fn);
console.log( myfn(1)(2) );const curry = function(fn){
return function(x){
return function(y){
return fn(x,y);
}
}
}
let myfn = curry(fn);
console.log( myfn(1)(2) );上面的curry函数只能处理二元情况,下面再来实现一个实现多参数的情况
// 多参数柯里化;
const curry = function(fn){
return function curriedFn(...args){
if(args.length<fn.length){
return function(){
return curriedFn(...args.concat([...arguments]));
}
}
return fn(...args);
}
}
const fn = (x,y,z,a)=>x+y+z+a;
const myfn = curry(fn);
console.log(myfn(1)(2)(3)(1));// 多参数柯里化;
const curry = function(fn){
return function curriedFn(...args){
if(args.length<fn.length){
return function(){
return curriedFn(...args.concat([...arguments]));
}
}
return fn(...args);
}
}
const fn = (x,y,z,a)=>x+y+z+a;
const myfn = curry(fn);
console.log(myfn(1)(2)(3)(1));关于柯里化函数的意义如下:
- 让纯函数更纯,每次接受一个参数,松散解耦
- 惰性执行
组合与管道
组合函数,目的是将多个函数组合成一个函数
举个简单的例子:
function afn(a){
return a*2;
}
function bfn(b){
return b*3;
}
const compose = (a,b)=>c=>a(b(c));
let myfn = compose(afn,bfn);
console.log( myfn(2));function afn(a){
return a*2;
}
function bfn(b){
return b*3;
}
const compose = (a,b)=>c=>a(b(c));
let myfn = compose(afn,bfn);
console.log( myfn(2));可以看到compose实现一个简单的功能:形成了一个新的函数,而这个函数就是一条从 bfn -> afn 的流水线
下面再来看看如何实现一个多函数组合:
const compose = (...fns)=>val=>fns.reverse().reduce((acc,fn)=>fn(acc),val);const compose = (...fns)=>val=>fns.reverse().reduce((acc,fn)=>fn(acc),val);compose执行是从右到左的。而管道函数,执行顺序是从左到右执行的
const pipe = (...fns)=>val=>fns.reduce((acc,fn)=>fn(acc),val);const pipe = (...fns)=>val=>fns.reduce((acc,fn)=>fn(acc),val);组合函数与管道函数的意义在于:可以把很多小函数组合起来完成更复杂的逻辑
三、优缺点
优点
更好的管理状态:因为它的宗旨是无状态,或者说更少的状态,能最大化的减少这些未知、优化代码、减少出错情况
更简单的复用:固定输入->固定输出,没有其他外部变量影响,并且无副作用。这样代码复用时,完全不需要考虑它的内部实现和外部影响
更优雅的组合:往大的说,网页是由各个组件组成的。往小的说,一个函数也可能是由多个小函数组成的。更强的复用性,带来更强大的组合性
隐性好处。减少代码量,提高维护性
缺点:
性能:函数式编程相对于指令式编程,性能绝对是一个短板,因为它往往会对一个方法进行过度包装,从而产生上下文切换的性能开销
资源占用:在 JS 中为了实现对象状态的不可变,往往会创建新的对象,因此,它对垃圾回收所产生的压力远远超过其他编程方式
递归陷阱:在函数式编程中,为了实现迭代,通常会采用递归操作