面试官:说说你对图的理解?相关操作有哪些?
一、是什么
在计算机科学中,图是一种抽象的数据类型,在图中的数据元素通常称为结点,V是所有顶点的集合,E是所有边的集合
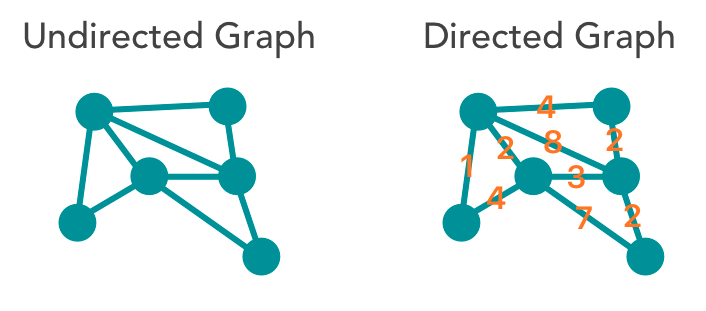
如果两个顶点v, w,只能由v向w,而不能由w向v,那么我们就把这种情况叫做一个从 v 到 w 的有向边。v 也被称做初始点,w也被称为终点。这种图就被称做有向图
如果v和w是没有顺序的,从v到达w和从w到达v是完全相同的,这种图就被称为无向图
图的结构比较复杂,任意两个顶点之间都可能存在联系,因此无法以数据元素在存储区中的物理位置来表示元素之间的关系
常见表达图的方式有如下:
邻接矩阵
邻接表
邻接矩阵
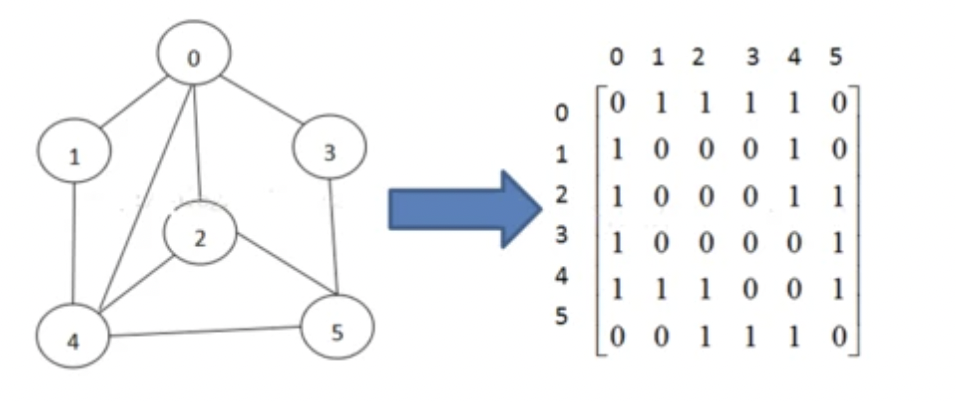
通过使用一个二维数组G[N][N]进行表示N个点到N-1编号,通过邻接矩阵可以立刻看出两顶点之间是否存在一条边,只需要检查邻接矩阵行i和列j是否是非零值,对于无向图,邻接矩阵是对称的
邻接表
存储方式如下图所示:
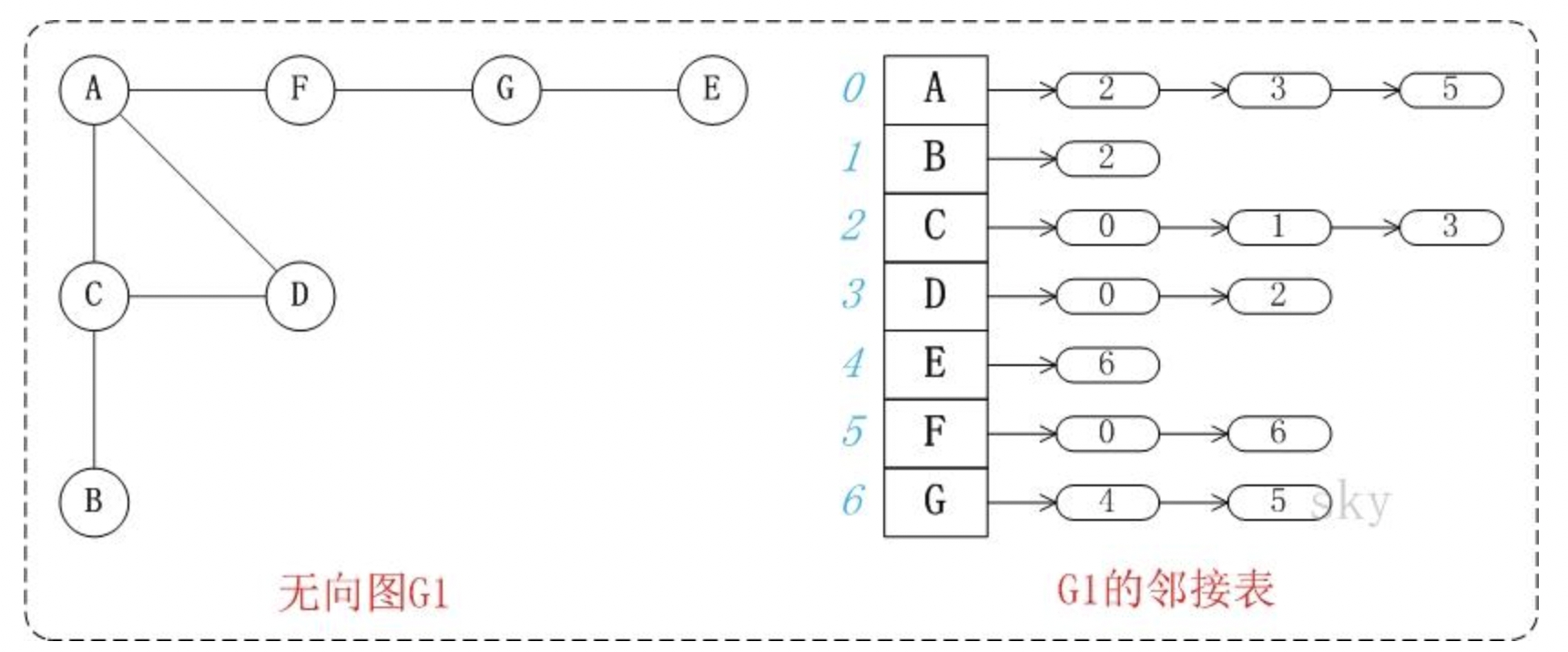
在javascript中,可以使用Object进行表示,如下:
const graph = {
A: [2, 3, 5],
B: [2],
C: [0, 1, 3],
D: [0, 2],
E: [6],
F: [0, 6],
G: [4, 5]
}const graph = {
A: [2, 3, 5],
B: [2],
C: [0, 1, 3],
D: [0, 2],
E: [6],
F: [0, 6],
G: [4, 5]
}图的数据结构还可能包含和每条边相关联的数值(edge value),例如一个标号或一个数值(即权重,weight;表示花费、容量、长度等)
二、操作
关于的图的操作常见的有:
- 深度优先遍历
- 广度优先遍历
首先构建一个图的邻接矩阵表示,如下面的图:
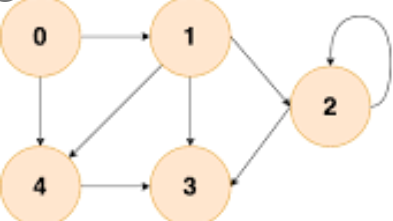
用代码表示则如下:
const graph = {
0: [1, 4],
1: [2, 4],
2: [2, 3],
3: [],
4: [3],
}const graph = {
0: [1, 4],
1: [2, 4],
2: [2, 3],
3: [],
4: [3],
}深度优先遍历
也就是尽可能的往深处的搜索图的分支
实现思路是,首先应该确定一个根节点,然后对根节点的没访问过的相邻节点进行深度优先遍历
确定以 0 为根节点,然后进行深度遍历,然后遍历1,接着遍历 2,然后3,此时完成一条分支0 - 1- 2- 3的遍历,换一条分支,也就是4,4后面因为3已经遍历过了,所以就不访问了
用代码表示则如下:
const visited = new Set()
const dfs = (n) => {
console.log(n)
visited.add(n) // 访问过添加记录
graph[n].forEach(c => {
if(!visited.has(c)){ // 判断是否访问呢过
dfs(c)
}
})
}const visited = new Set()
const dfs = (n) => {
console.log(n)
visited.add(n) // 访问过添加记录
graph[n].forEach(c => {
if(!visited.has(c)){ // 判断是否访问呢过
dfs(c)
}
})
}广度优先遍历
先访问离根节点最近的节点,然后进行入队操作,解决思路如下:
- 新建一个队列,把根节点入队
- 把队头出队并访问
- 把队头的没访问过的相邻节点入队
- 重复二、三步骤,知道队列为空
用代码标识则如下:
const visited = new Set()
const dfs = (n) => {
visited.add(n)
const q = [n]
while(q.length){
const n = q.shift()
console.log(n)
graph[n].forEach(c => {
if(!visited.has(c)){
q.push(c)
visited.add(c)
}
})
}
}const visited = new Set()
const dfs = (n) => {
visited.add(n)
const q = [n]
while(q.length){
const n = q.shift()
console.log(n)
graph[n].forEach(c => {
if(!visited.has(c)){
q.push(c)
visited.add(c)
}
})
}
}三、总结
通过上面的初步了解,可以看到图就是由顶点的有穷非空集合和顶点之间的边组成的集合,分成了无向图与有向图
图的表达形式可以分成邻接矩阵和邻接表两种形式,在javascript中,则可以通过二维数组和对象的形式进行表达
图实际是很复杂的,后续还可以延伸出无向图和带权图,对应如下图所示: